¶ 2004 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2004 AIME II problems here.
Discussion Forum
Engage in discussion about the 2004 AIME II math contest by visiting Random Math AIME II 2004 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2004 AIME II problems, please refer below:
Problem 1: A chord of a circle is perpendicular to a radius at the midpoint of the radius. The ratio of the area of the larger of the two regions into which the chord divides the circle to the smaller can be expressed in the form , where , , and are positive integers, and are relatively prime, and neither nor is divisible by the square of any prime. Find the remainder when the product is divided by .
Solution:
Problem 2: A jar has red candies and blue candies. Terry picks two candies at random, then Mary picks two of the remaining candies at random. Given that the probability that they get the same color combination, irrespective of order, is , where and are relatively prime positive integers, find .
Solution:
Problem 3: A solid rectangular block is formed by gluing together congruent -cm cubes face to face. When the block is viewed so that three of its faces are visible, exactly of the -cm cubes cannot be seen. Find the smallest possible value of .
Solution:
Problem 4: How many positive integers less than have at most two different digits?
Solution:
Problem 5: In order to complete a large job, workers were hired, just enough to complete the job on schedule. All the workers stayed on the job while the first quarter of the work was done, so the first quarter of the work was completed on schedule. Then workers were laid off, so the second quarter of the work was completed behind schedule. Then an additional workers were laid off, so the third quarter of the work was completed still further behind schedule. Given that all workers work at the same rate, what is the minimum number of additional workers, beyond the workers still on the job at the end of the third quarter, that must be hired after three-quarters of the work has been completed so that the entire project can be completed on schedule or before?
Solution:
Problem 6: Three clever monkeys divide a pile of bananas. The first monkey takes some bananas from the pile, keeps three-fourths of them, and divides the rest equally between the other two. The second monkey takes some bananas from the pile, keeps one-fourth of them, and divides the rest equally between the other two. The third monkey takes the remaining bananas from the pile, keeps one-twelfth of them, and divides the rest equally between the other two. Given that each monkey receives a whole number of bananas whenever the bananas are divided, and the numbers of bananas the first, second, and third monkeys have at the end of the process are in the ratio , what is the least possible total for the number of bananas?
Solution:
Problem 7: is a rectangular sheet of paper that has been folded so that corner is matched with point on edge . The crease is , where is on and is on . The dimensions , and are given. The perimeter of rectangle is , where and are relatively prime positive integers. Find .
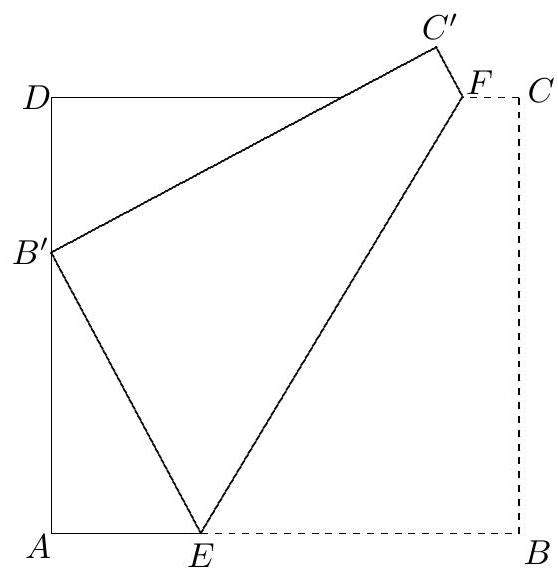
Solution:
Problem 8: How many positive integer divisors of are divisible by exactly positive integers?
Solution:
Problem 9: A sequence of positive integers with and is formed so that the first three terms are in geometric progression, the second, third, and fourth terms are in arithmetic progression, and, in general, for all , the terms , and are in geometric progression, and the terms , , and are in arithmetic progression. Let be the greatest term in this sequence that is less than . Find .
Solution:
Problem 10: Let be the set of integers between and whose binary expansions have exactly two 's. If a number is chosen at random from , the probability that it is divisible by is , where and are relatively prime positive integers. Find .
Solution:
Problem 11: A right circular cone has a base with radius and height . A fly starts at a point on the surface of the cone whose distance from the vertex of the cone is , and crawls along the surface of the cone to a point on the exact opposite side of the cone whose distance from the vertex is . Find the least distance that the fly could have crawled.
Solution:
Problem 12: Let be an isosceles trapezoid, whose dimensions are , and . Draw circles of radius centered at and , and circles of radius centered at and . A circle contained within the trapezoid is tangent to all four of these circles. Its radius is , where , and are positive integers, is not divisible by the square of any prime, and and are relatively prime. Find .
Solution:
Problem 13: Let be a convex pentagon with , , and . Given that the ratio between the area of and the area of is , where and are relatively prime positive integers, find .
Solution:
Problem 14: Consider a string of 's, , into which signs are inserted to produce an arithmetic expression. For example, could be obtained from eight 's in this way. For how many values of is it possible to insert signs so that the resulting expression has value
Solution:
Problem 15: A long thin strip of paper is units in length, unit in width, and is divided into unit squares. The paper is folded in half repeatedly. For the first fold, the right end of the paper is folded over to coincide with and lie on top of the left end. The result is a by strip of double thickness. Next, the right end of this strip is folded over to coincide with and lie on top of the left end, resulting in a by strip of quadruple thickness. This process is repeated more times. After the last fold, the strip has become a stack of unit squares. How many of these squares lie below the square that was originally the nd square counting from the left?
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions