¶ 2008 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2008 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2008 AMC 10B math contest by visiting Random Math AMC 10B 2008 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2008 AMC 10B problems, please refer below:
Problem 1: A basketball player made baskets during a game. Each basket was worth either or points. How many different numbers could represent the total points scored by the player?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A block of calendar dates is shown. The order of the numbers in the second row is to be reversed. Then the order of the numbers in the fourth row is to be reversed. Finally, the numbers on each diagonal are to be added. What will be the positive difference between the two diagonal sums?
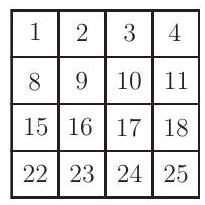
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Assume that is a positive real number. Which is equivalent to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A semipro baseball league has teams with players each. League rules state that a player must be paid at least , and that the total of all players' salaries for each team cannot exceed . What is the maximum possible salary, in dollars, for a single player?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: For real numbers and , define . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Points and lie on . The length of is times the length of , and the length of is times the length of . The length of is what fraction of the length of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: An equilateral triangle of side length is completely filled in by non-overlapping equilateral triangles of side length . How many small triangles are required?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A class collects to buy flowers for a classmate who is in the hospital. Roses each, and carnations cost each. No other flowers are to be used. How many different bouquets could be purchased for exactly ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A quadratic equation has two real solutions. What is the average of the solutions?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Points and are on a circle of radius and . Point is the midpoint of the minor arc . What is the length of the line segment ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Suppose that is a sequence of real numbers satisfying , and that and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Postman Pete has a pedometer to count his steps. The pedometer records up to steps, then flips over to on the next step. Pete plans to determine his mileage for a year. On January Pete sets the pedometer to . During the year, the pedometer flips from to forty-four times. On December the pedometer reads . Pete takes steps per mile. Which of the following is closest to the number of miles Pete walked during the year?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: For each positive integer , the mean of the first terms of a sequence is . What is the th term of the sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Triangle has , and in the first quadrant. In addition, and . Suppose that is rotated counterclockwise about . What are the coordinates of the image of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: How many right triangles have integer leg lengths and and a hypotenuse of length , where ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Two fair coins are to be tossed once. For each head that results, one fair die is to be rolled. What is the probability that the sum of the die rolls is odd? (Note that if no die is rolled, the sum is .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A poll shows that of all voters approve of the mayor's work. On three separate occasions a pollster selects a voter at random. What is the probability that on exactly one of these three occasions the voter approves of the mayor's work?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Bricklayer Brenda would take hours to build a chimney alone, and bricklayer Brandon would take hours to build it alone. When they work together, they talk a lot, and their combined output is decreased by bricks per hour. Working together, they build the chimney in hours. How many bricks are in the chimney?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A cylindrical tank with radius feet and height feet is lying on its side. The tank is filled with water to a depth of feet. What is the volume of the water, in cubic feet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The faces of a cubical die are marked with the numbers , and . The faces of a second cubical die are marked with the numbers , and . Both dice are thrown. What is the probability that the sum of the two top numbers will be , or ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Ten chairs are evenly spaced around a round table and numbered clockwise from through . Five married couples are to sit in the chairs with men and women alternating, and no one is to sit either next to or directly across from his or her spouse. How many seating arrangements are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Three red beads, two white beads, and one blue bead are placed in a line in random order. What is the probability that no two neighboring beads are the same color?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A rectangular floor measures feet by feet, where and are positive integers with . An artist paints a rectangle on the floor with the sides of the rectangle parallel to the sides of the floor. The unpainted part of the floor forms a border of width foot around the painted rectangle and occupies half the area of the entire floor. How many possibilities are there for the ordered pair ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Quadrilateral has , , and . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Michael walks at the rate of feet per second on a long straight path. Trash pails are located every feet along the path. A garbage truck travels at feet per second in the same direction as Michael and stops for seconds at each pail. As Michael passes a pail, he notices the truck ahead of him just leaving the next pail. How many times will Michael and the truck meet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions