¶ 2013 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2013 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2013 AMC 10B math contest by visiting Random Math AMC 10B 2013 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2013 AMC 10B problems, please refer below:
Problem 1: What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Mr. Green measures his rectangular garden by walking two of the sides and finds that it is steps by steps. Each of Mr. Green's steps is feet long. Mr. Green expects a half a pound of potatoes per square foot from his garden. How many pounds of potatoes does Mr. Green expect from his garden?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: On a particular January day, the high temperature in Lincoln, Nebraska, was degrees higher than the low temperature, and the average of the high and low temperatures was . In degrees, what was the low temperature in Lincoln that day?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: When counting from to is the number counted. When counting backwards from to is the number counted. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Positive integers and are each less than . What is the smallest possible value for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The average age of fifth-graders is . The average age of of their parents is . What is the average age of all of these parents and fifth-graders?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Six points are equally spaced around a circle of radius . Three of these points are the vertices of a triangle that is neither equilateral nor isosceles. What is the area of this triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Ray's car averages miles per gallon of gasoline, and Tom's car averages miles per gallon of gasoline. Ray and Tom each drive the same number of miles. What is the cars' combined rate of miles per gallon of gasoline?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Three positive integers are each greater than , have a product of , and are pairwise relatively prime. What is the sum of these integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A basketball team's players were successful on of their two-point shots and of their three-point shots, which resulted in points. They attempted more two-point shots than three-point shots. How many three-point shots did they attempt?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Real numbers and satisfy the equation . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let be the set of sides and diagonals of a regular pentagon. A pair of elements of are selected at random without replacement. What is the probability that the two chosen segments have the same length?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Jo and Blair take turns counting from to one more than the last number said by the other person. Jo starts by saying "", so Blair follows by saying "". Jo then says "", and so on. What is the number said?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Define . Which of the following describes the set of points for which ?
Answer Choices:
A. a finite set of points
B. one line
C. two parallel lines
D. two intersecting lines
E. three lines
Solution:
Problem 15: A wire is cut into two pieces, one of length and the other of length . The piece of length is bent to form an equilateral triangle, and the piece of length is bent to form a regular hexagon. The triangle and the hexagon have equal area. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
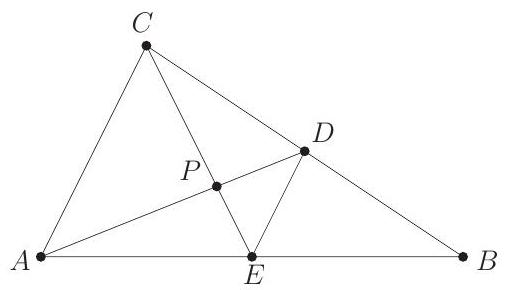
Problem 16: In , medians and intersect at , and . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Alex has red tokens and blue tokens. There is a booth where Alex can give two red tokens and receive in return a silver token and a blue token, and another booth where Alex can give three blue tokens and receive in return a silver token and a red token. Alex continues to exchange tokens until no more exchanges are possible. How many silver tokens will Alex have at the end?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The number has the property that its units digit is the sum of its other digits, that is . How many integers less than but greater than share this property?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The real numbers form an arithmetic sequence with . The quadratic has exactly one root. What is this root?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The number is expressed in the form
where and are positive integers and is as small as possible. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two non-decreasing sequences of nonnegative integers have different first terms. Each sequence has the property that each term beginning with the third is the sum of the previous two terms, and the seventh term of each sequence is . What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
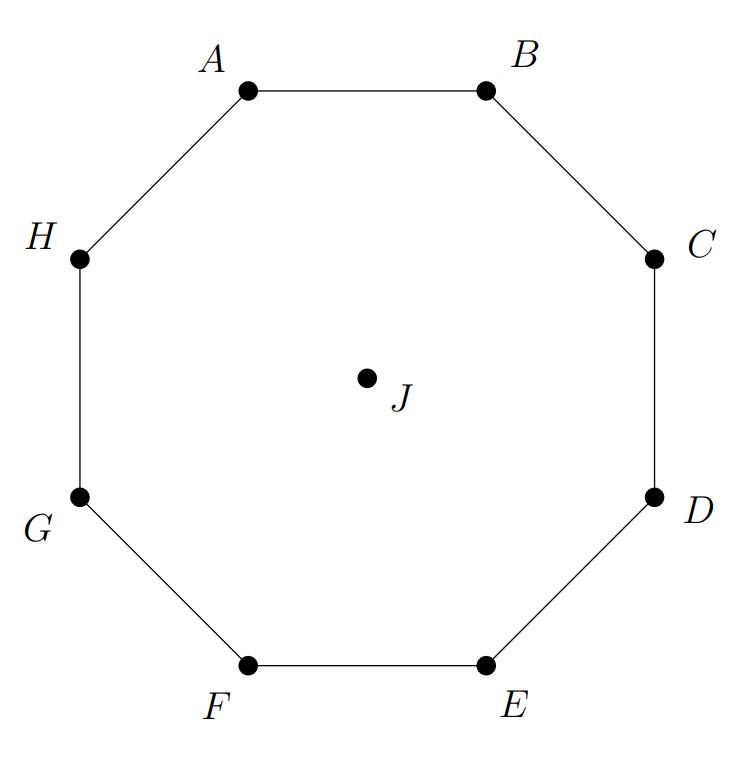
Problem 22: The regular octagon has its center at . Each of the vertices and the center are to be associated with one of the digits through , with each digit used once, in such a way that the sums of the numbers on the lines , , , and are equal. In how many ways can this be done?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: In triangle , and . Distinct points , and lie on segments , and , respectively, such that , , and . The length of segment can be written as , where and are relatively prime positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A positive integer is nice if there is a positive integer with exactly four positive divisors (including and ) such that the sum of the four divisors is equal to . How many numbers in the set are nice?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Bernardo chooses a three-digit positive integer and writes both its base- and base- representations on a blackboard. Later LeRoy sees the two numbers Bernardo has written. Treating the two numbers as base- integers, he adds them to obtain an integer . For example, if , Bernardo writes the numbers and , and LeRoy obtains the sum . For how many choices of are the two rightmost digits of , in order, the same as those of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions