¶ 2016 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2016 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2016 AMC 12B math contest by visiting Random Math AMC 12B 2016 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2016 AMC 12B problems, please refer below:
Problem 1: What is the value of
when ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The harmonic mean of two numbers can be computed as twice their product divided by their sum. The harmonic mean of and is closest to which integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Let . What is the value of || ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The ratio of the measures of two acute angles is , and the complement of one of these two angles is twice as large as the complement of the other. What is the sum of the degree measures of the two angles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The War of started with a declaration of war on Thursday, June . The peace treaty to end the war was signed days later, on December . On what day of the week was the treaty signed?
Answer Choices:
A. Friday
B. Saturday
C. Sunday
D. Monday
E. Tuesday
Solution:
Problem 6: All three vertices of lie on the parabola defined by , with at the origin and parallel to the -axis. The area of the triangle is . What is the length ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Josh writes the numbers . He marks out , skips the next number , marks out , and continues skipping and marking out the next number to the end of his list. Then he goes back to the start of his list, marks out the first remaining number , skips the next number , marks out , skips , marks out , and so on to the end. Josh continues in this manner until only one number remains. What is that number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A thin piece of wood of uniform density in the shape of an equilateral triangle with side length inches weighs ounces. A second piece of the same type of wood, with the same thickness, also in the shape of an equilateral triangle, has side length inches. Which of the following is closest to the weight, in ounces, of the second piece?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Carl decided to fence in his rectangular garden. He bought fence posts, placed one on each of the four corners, and spaced out the rest evenly along the edges of the garden, leaving exactly yards between neighboring posts. The longer side of his garden, including the corners, has twice as many posts as the shorter side, including the corners. What is the area, in square yards, of Carl's garden?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A quadrilateral has vertices , and , where and are integers with . The area of is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: How many squares whose sides are parallel to the axes and whose vertices have coordinates that are integers lie entirely within the region bounded by the line , the line , and the line ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: All the numbers are written in a array of squares, one number in each square, in such a way that if two numbers are consecutive then they occupy squares that share an edge. The numbers in the four corners add up to . What number is in the center?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Alice and Bob live miles apart. One day Alice looks due north from her house and sees an airplane. At the same time Bob looks due west from his house and sees the same airplane. The angle of elevation of the airplane is from Alice's position and from Bob's position. Which of the following is closest to the airplane's altitude, in miles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The sum of an infinite geometric series is a positive number , and the second term in the series is . What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: All the numbers are assigned to the six faces of a cube, one number to each face. For each of the eight vertices of the cube, a product of three numbers is computed, where the three numbers are the numbers assigned to the three faces that include that vertex. What is the greatest possible value of the sum of these eight products?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: In how many ways can be written as the sum of an increasing sequence of two or more consecutive positive integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In shown in the figure, , and is an altitude. Points and lie on sides and , respectively, so that and are angle bisectors, intersecting at and , respectively. What is
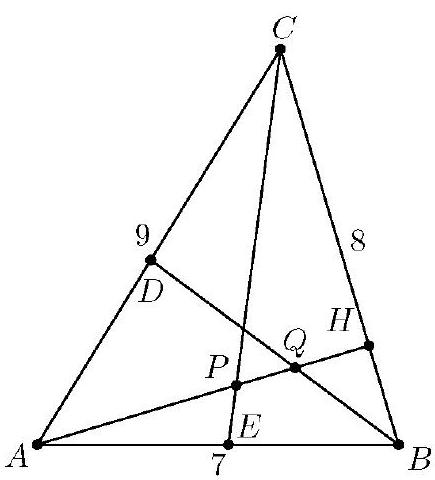
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: What is the area of the region enclosed by the graph of the equation ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Tom, Dick, and Harry are playing a game. Starting at the same time, each of them flips a fair coin repeatedly until he gets his first head, at which point he stops. What is the probability that all three flip their coins the same number of times?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A set of teams held a round-robin tournament in which every team played every other team exactly once. Every team won games and lost games; there were no ties. How many sets of three teams were there in which beat beat , and beat ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let be a unit square. Let be the midpoint of . For , let be the intersection of and , and let be the foot of the perpendicular from to . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: For a certain positive integer less than , the decimal equivalent of is , a repeating decimal of period , and the decimal equivalent of is , a repeating decimal of period . In which interval does lie?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: What is the volume of the region in three-dimensional space defined by the inequalities and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: There are exactly ordered quadruples such that and . What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The sequence is defined recursively by , and for . What is the smallest positive integer such that the product is an integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions