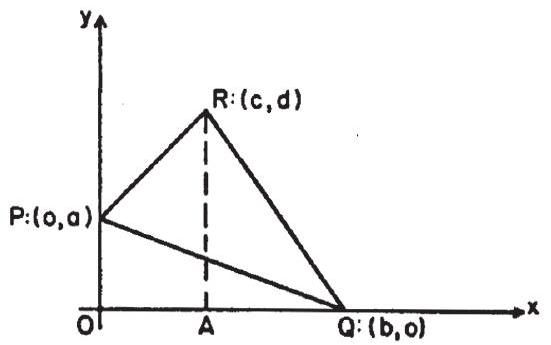
Problem: The vertices of triangle PQR have coordinates as follows: P(o,a),Q(b,o),R(c,d), where a,b,c and d are positive. The area of triangle PQR may be found from the expression:
Answer Choices:
A. 2ab+ac+bc+cd
B. 2ac+bd−ab
C. 2ab−ac−bd
D. 2ac+bd+ab
E. 2ac+bd−ab−cd
Solution:
From R:(c,d), draw line segment RA perpendicular to the x-axis. Let O denote the origin (0,0).
If c>b,
area △PQR= area trapezoid OPRA− area △QAR - area △OPQ
=21c(a+d)−21d(c−b)−21ab=21(ac+bd−ab).
If c<b,
area △PQR= area trapezoid OPRA+ area △QAR− area △OPQ
=21c(a+d)+21d(b−c)−21ab=21(ac+bd−ab).
.jpg)