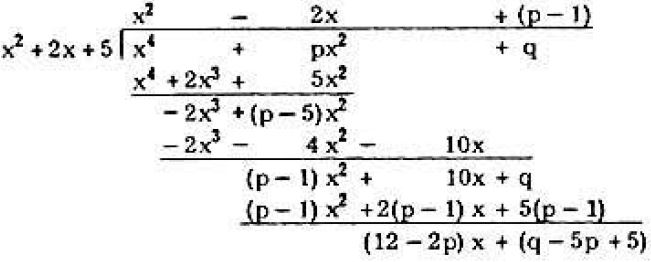Problem: For x2+2x+5 to be a factor of x4+px2+q, the values of p and q must be, respectively:
Answer Choices:
A. −2,5
B. 5,25
C. 10,20
D. 6,25
E. 14,25
Solution:
Let the other factor be x2+ax+b. Then
(x2+2x+5)(x2+ax+b)≡x4+x3(2+a)+x2(5+b+2a)+x(5a+2b)+5b≡x4+px2+q
Match the coefficients of like powers of x
For x3xx2x3we have 2+a=05a+2b=05+b+2a=p5b=q∴a=−2∴b=5∴p=6∴q=25
or
Let y=x2 so that x4+px2+q=y2+py+q. Let the roots of y2+py+q=0 be r2 and s2. Since y=x2 the roots of x4+px2+q=0 must be ±r,±s. Now x2+2x+5 is a factor of x4+px2+q; consequently, one pair of roots, say r and s, must satisfy the equation x2+2x+5=0. It follows that −r and −s must satisfy the equation x2−2x+5=0. Therefore, the other factor must be x2−2x+5. ∴(x2+2x+5)(x2−2x+5)≡x4+6x2+25≡x4+px2+q ∴p=6,q=25
Since the reminder must be zero (why?) 12−2p=0,p=6 and q−5p+5=0,q=25