Problem: Let the bisectors of the exterior angles at B and C of triangle ABC meet at D. Then, if all measurements are in degrees, angle BDC equals:
Answer Choices:
A. 21(90−A)
B. 90−A
C. 21(180−A)
D. 180−A
E. 180−2 A
Solution:
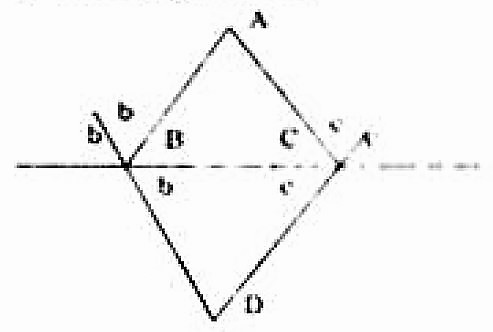
2∠b2∠c∴∠b+∠c But (∠B+∠C)∴∠b+∠c∠BDC=180∘−∠B=180∘−∠C=180∘−21(∠B+∠C)=180∘−∠A=180∘−21(180∘−∠A)=180∘−(∠b+∠c)=180∘−(180∘−21(180∘−∠A))=21(180∘−∠A)

