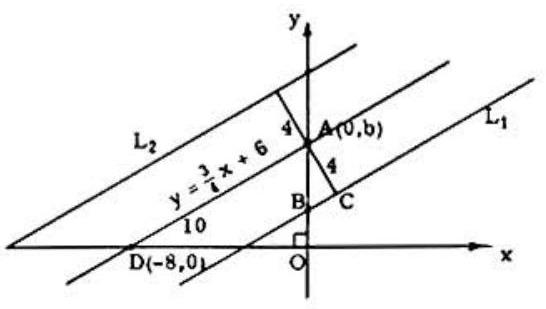
Problem: Given the line y=43x+6 and a line L parallel to the given line and 4 units from it. A possible equation for L is:
Answer Choices:
A. y=43x+1
B. y=43x
C. y=43x−32
D. y=43x−1
E. y=43x+2
Solution:
There are two possibilities, L1 and L2. The methods for finding the equation of L2 are similar to the methods for finding the equation of L1 shown here: Since L1 is parallel to the line y=43x+6, its equation is y=43x+b, where b, the y-intercept, is to be determined. Since △ABC∼△DAO,ADAB=DOAC, so that 10AB=84 and AB=5. Hence, b=1 and the equation of L1 is y=43x+1.
\includegraphics[max width=\textwidth]
or
Let d1 be the distance from the origin to L1 and let d2 be the distance from the origin to the given line. Then d1=54b and d2=524.∴d2−d1=524−54b=4, and b=1.