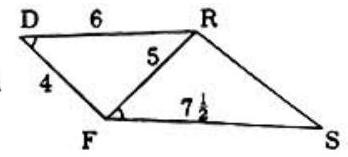
Problem: In this figure ∠RFS=∠FDR,FD=4 inches, DR= 6 inches, FR=5 inches, FS=721 inches. The length of RS, in inches is:
Answer Choices:
A. undetermined
B. 4
C. 521
D. 6
E. 641
Solution:
△RFD∼△RSF (an angle of one triangle equal to an angle of the other triangle and the including sides in proportion).
∴RFRS=RDSF,5RS=6721,RS=641
OR
by the law of cosines, 52=42+62−2⋅4⋅6cos∠D
∴cos∠D=4827=cos∠RFS
\therefore RS^{2}=5^{2}+\left(7 \dfrac{1}{2}\right)^{2}-2\left(7 \dfrac{1}{2}\right)(5)\left(\dfrac{27}{48}\right) \quad \therefore \mathrm{RS}=6 \dfrac{1}