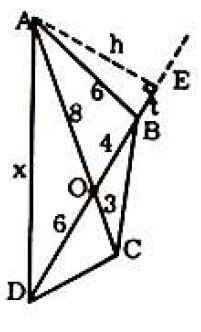
Problem: In quadrilateral ABCD with diagonals AC and BD, intersecting at O,BO=4, OD=6,AO=8,OC=3, and AB=6. The length of AD is:
Answer Choices:
A. 9
B. 10
C. 63
D. 82
E. 166
Solution:
82=h2+(4+t)2,62=h2+t2,t=23
∴h=2315∴x2=h2+DE2=4135+4529=166∴x=166.
or
△BOC∼△AOD with side ratio 1:2∴BC=21x
△AOB∼△DOC∴CD=421. Since ABCD is inscriptible (why?) we may use Ptolemy's Theorem.
∴x⋅2x+6⋅421=(6+4)(8+3)∴x=166.