Problem: Points D,E,F are taken respectively on sides AB,BC, and CA of triangle ABC so that AD:DB=BE:CE=CF:FA=1:n. The ratio of the area of triangle DEF to that of triangle ABC is:
Answer Choices:
A. (n+1)2n2−n+1
B. (n+1)21
C. (n+1)32n3
D. (n+1)3n3
E. n+1n(n−1)
Solution:
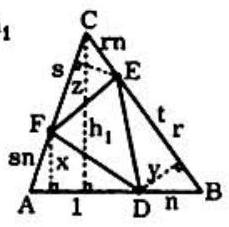
Designate AD by 1, DB by n1,BE by r,EC by rn, CF by s , and FA by sn. Let h1 be the altitude from C,h2, the altitude from A, and h3, the altitude from B.
By similar triangles h1x=sn+ssn=1+nn∴x=1+nnh1
∴ area (△ADF)=21(1)(x)=211+nnh1. In a like manner y=1+nnh2 and area
(△BDE)=211+nrnh2, and z=1+nnh3 and area (△CFE)=211+nsnh3.
But the area (△ABC)=31⋅21[h1(1+n)+h2(1+n)r+h3(1+n)s]=61(1+n)(h1+h2r+h3s)
∴area(△DEF)=61(1+n)(h1+h2r+h3s)−211+nn(h1+h2r+h3s)=6(1+n)n2−n+1(h1+h2r+h3s)
∴ the required ratio is (n+1)2n2−n+1.
Draw DG|AC. By similar triangles BCBG=1+nn∴BG=1+nnBC=1+nn⋅r(1+n)=nr. Also, letting K be the area of △ABC, we have K area (△DBG)=(1+n)2n2
∴ area (△DBG)=(1+n)2n2K. Since △BDE has base r and altitude equal to that of △BDG,area(△BDG) area (△BDE)=BGr=rnr=n1∴ area (△BDE)=n1⋅(1+n)2n2K =(1+n)2nK. In like manner (△ECF)=(1+n)2nK and area (△ADF)=(1+n)2nK.
∴ area (△DEF)=K−(1+n)23nK=(n+1)2n2−n+1K.
.jpg)

.jpg)