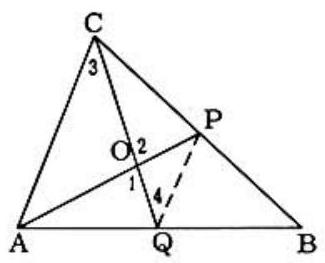
Problem: Let O be the intersection point of medians AP and CQ of triangle ABC. If OQ is 3 inches, then OP, in inches, is:
Answer Choices:
A. 3
B. 29
C. 6
D. 9
E. undetermined
Solution:
Since OQ=3,CQ=9. But OP=31AP and we can establish an arbitrary length for AP and, hence, for OP, as follows:
Draw CQ=9 with OQ=3. Through O draw OP of any length and extend PO through O to A so that AP =3(OP). Point B is then the intersection of AQ and CP and, thus, △ABC has AP and CQ as medians:
(1) OPAO=OQCO,∠1=∠2,△AOC∼△POQ
(2) ∴QPAC=OQCO=12,∠3=∠4,QP∥AC
(3) ∴QBAB=PBCB=QPAC=12 so that Q,P are midpoints.