Problem: Let P be a point of hypotenuse AB (or its extension) of isosceles right triangle ABC. Let s=AP2+PB2. Then:
Answer Choices:
A. s<2CP2 for a finite number of positions of P
B. s<2CP2 for an infinite number of positions of P
C. s=2CP2 only if P is the midpoint of AB or an endpoint of AB
D. s=2CP2 always
E. s>2CP2 if P is a trisection point of AB
Solution:
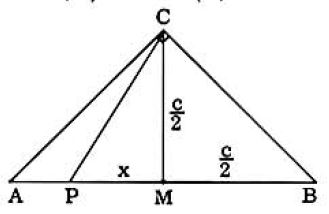
Method I. (see fig. 1) Let M be the midpoint of hypotenuse c . Then S=AP2+PB2= (2c−x)2+(2c+x)2=2c2=2x2. But x2=CP2−(2c)2
∴S=2c2+2CP2−2c2=2CP2
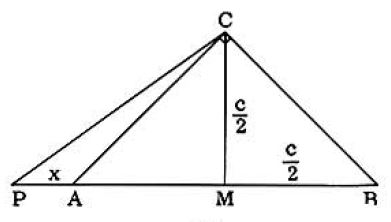
(see fig. 2) S=AP2+PB2=
x2+(c+x)2=c2+2cx+2x2. But CP2=(x+2c)2+(2c)2=
x2+cx+2c2.∴s=2CP2
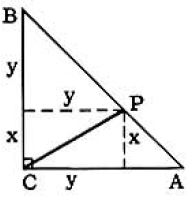
Method II. (for P interior to AB, fig. 3)
S=AP2+PB2,AP2=x2+x2=2x2, PB2= y2+y2=2y2.∴S=2x2+2y2=2(x2+y2)= 2CP2
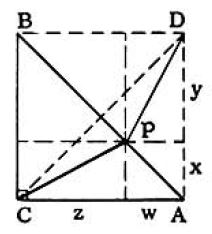
Method III. (for P interior to AB, fig. 4)
Complete △ACB to square ACBD. Draw PD and draw perpendiculars from P to AC,CB, BD,DA.AP2=x2+w2,BP2=y2+z2,CP2= x2+z2,DP2=y2+w2,∴AP2+BP2=x2+y2+z2+w2,CP2+DP2=x2+y2+z2+w2 ∴S=AP2+BP2=CP2+DP2. But DP=CP (Why?) ∴S=2CP2