Problem: Let OABC be a unit square in the xy-plane with O(0,0),A(1,0),B(1,1) and C(0,1). Let u=x2−y2 and v=2xy be a transformation of the xy-plane into the uv-plane. The transform (or image) of the square is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
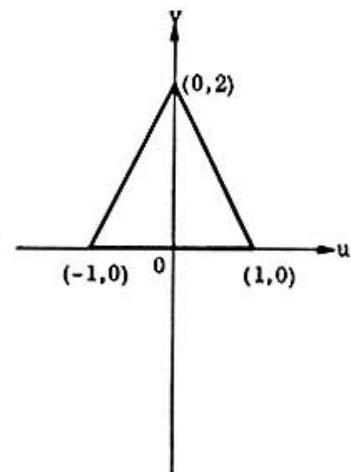
The image of A(1,0) in the xy-plane is A′(1,0) in the uvplane since u=12−02 =1 and v=2(1)(0)=0. The image of B(1,1) is B′(0,2), the image of C(0,1) is C′(−1,0), and the image of O(0,0) is O′(0,0).
The image of the straight line AB whose xy− equation is x=1 is the parabolic arcA′B′ whose uv- equation is v2=4(1−u), a parabola, since u=1−y2 and v=2y. The image of the straight line OA (equation y=0 ) is the straight line O′A′ (equations v=0,u=x2 ), and the image of the straight line OC (equation x=0 ) is the straight line O′C′ (equations v=0,u=−y2 ).
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)