¶ 1971 AHSME Problem 5
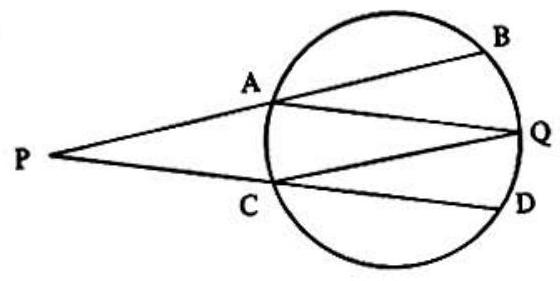
Problem: Points , and lie on the circle shown and the measures of arcs and are and respectively. The sum of the measures of angles and is
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem: Points , and lie on the circle shown and the measures of arcs and are and respectively. The sum of the measures of angles and is

Answer Choices:
A.
B.
C.
D.
E. None of these
Solution: