¶ 1973 AHSME Problem 35
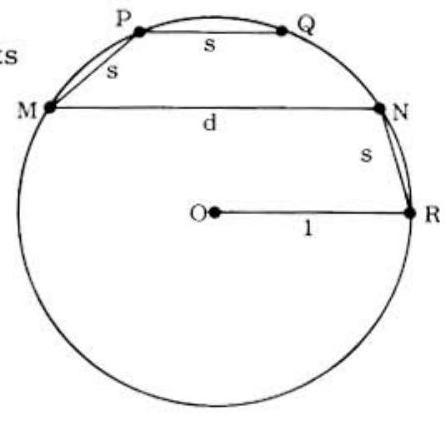
Problem: In the unit circle shown in the figure to the right, chords and are parallel to the unit radius of the circle with center at . Chords and are each units long and chord is units long. Of the three equations
I. ,
II. ds ,
III.
those which are necessarily true are
Answer Choices:
A. I only
B. II only
C. III only
D. I and II only
E. I, II, and III
Solution:
Chord has length (See figure) and each chord of length a subtends an arc of . Draw a radius meeting at . Also draw perpendicular and to from and reapectively. Triangles and are similar so that
or , Therefore
To see thet , note that because . Also so that is a parallelogram with opposite sides . . Now or and .. All three of the equations I, II, and III are necessarily true as stated in choice (E).
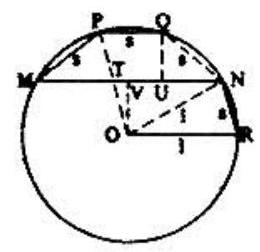
or
Alternately, follows from and because is a parallelogram with side . Now let (not shown) danote the other and of the diameter through . Then chords and intersect at and the products of their segments are equal.
or
This quadratic equation iess the pooitive root from which relations II and III can be verified. Therefore all three equations I , II and III are pecessarily true.