¶ 1974 AHSME Problem 16
Problem: A circle of radius is inscribed in a right isosceles triangle, and a circle of radius is circumscribed about the triangle. Then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
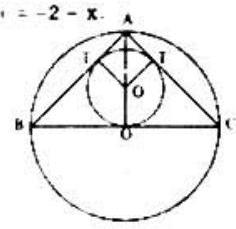
In the adjoining figure. a right isosceles triangle, with and , Inscribed in a circle with center and radius The line segment AO has length and bisects line segment and . A circle with center lying on and radius is inscribed in . The sides and are tangent to the inscribed circle with points of tangency and , respectively. Since has angles and , and , then and .