¶ 1975 AHSME Problem 20
Problem: In the adjoining figure triangle is such that and . If is the midpoint of and , what is the length of
Answer Choices:
A.
B.
C.
D. not enough information
E. 9 given to solve the problem
Solution:
In the adjoining figure let be the length of altitude drawn to , let and let . Then
Subtracting twice the second equation from the sum of the first and third equations yields . Thus and .
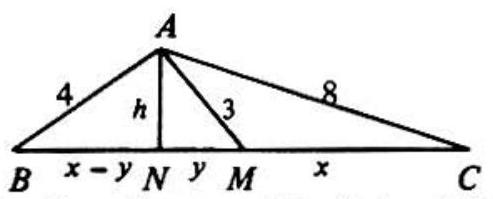
OR
Applying the parallelogram law to the parallelogram having and as adjacent sides yields
\includegraphics[max width=\textwidth]