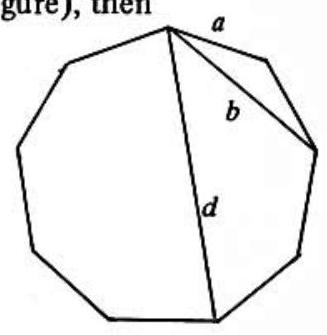
Problem: If a,b and d are the lengths of a side, a shortest diagonal and a longest diagonal, respectively, of a regular nonagon, then
Answer Choices:
A. d=a+b
B. d2=a2+b2
C. d2=a2+ab+b2
D. b=2a+d
E. b2=ad
Solution:
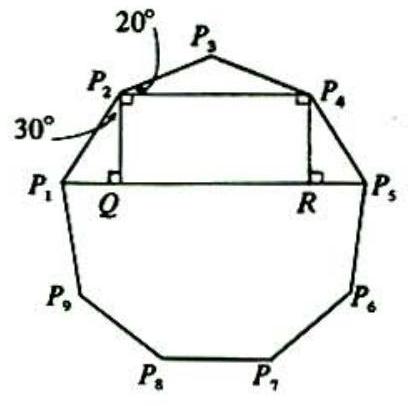
In the adjoining figure, P1P2⋯P9 is a regular nonagon; P1P2=a; P2P4=b;P1P5=d;Q and R lie on P1P5;P2Q⊥P1P5;P4R⊥P1P5. Since P2P3=P3P4 and the interior angles of a regular nonagon are each
(9180(9−2))∘=140∘
∠P3P2P4=20∘. Hence ∠P1P2Q=30∘ and P1Q=2a. Similarly, P5R=2a. Thus d=a+b.