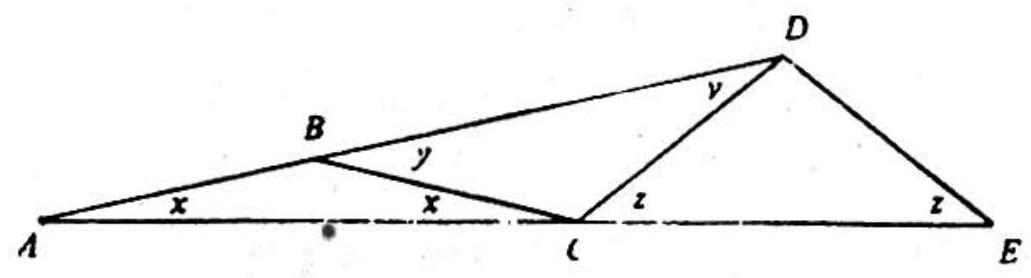
Problem: In △ADE,∠ADE=140∘ and points B and C lie on sides AD and AE, respectively. If lengths AB,BC,CD and DE are all equal, then the measure of ∠EAD is
Answer Choices:
A. 5∘
B. 6∘
C. 7.5∘
D. 8∘
E. 10∘
Solution:
Let x=△BAC=∠BCA;y=∠CBD=∠CDB and z=∠DCE=∠DEC. Applying the theorem on exterior angles to △ABC and △ACD and the theorem on the surn of the interior angles of a triangle to △ADE yields
yz=x+yx+∠ADE+z140+4xx=2x=3x=180=180=10.