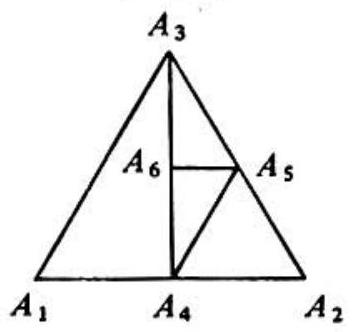
Problem: If ΔA1A2A3 is equilateral and An+3 is the midpoint of line segment AnAn+1 for all positive integers n, then the measure of X44A45A43 equals
Answer Choices:
A. 30∘
B. 45∘
C. 60∘
D. 90∘
E. 120∘
Solution:
Triangle A2A3A4 has vertex angles 60∘,30∘. 90∘, respectively. Since ∠A1A2A3=60∘, and A2A4 and A2A5 have the same length, ΔA2A4A5 is equilateral. Therefore, ΔA3A4A5 has vertex angles 30∘,30∘,120∘. respectively. Then ΔA4A5A6 has vertex angles 30∘,60∘,90∘, respectively.
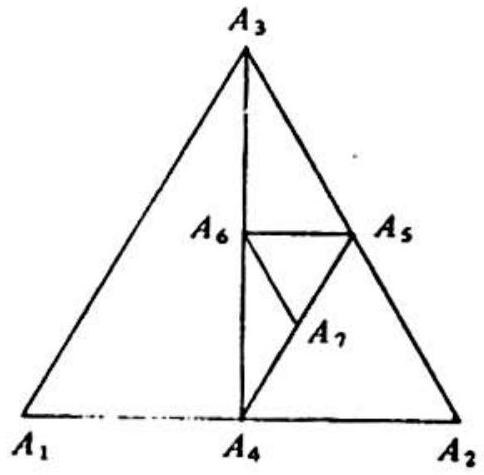
Finally, since A4A5A6=60∘ and A5A6 and A5A7 have the same length, △A5A6A7 is again equilateral. Therefore △AnAn+1An+2 ∼ΔAn+4An+5An+6 with An and An+4 as corresponding vertices. Thus ∠A44A45A43=∠A4A5A3=120∘.