¶ 1979 AHSME Problem 12
Problem: In the adjoining figure, is the diameter of a semi-circle with center . Point lies on the extension of past ; point lies on the semi-circle, and is the point of intersection (distinct from ) of line segment : with the semi-circle. If length equals length , and the measure of is , then the measure of is
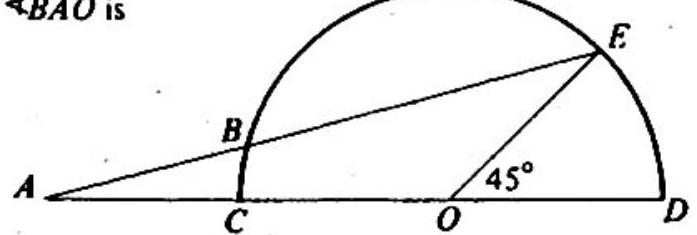
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Draw line segment BO, and let and denote the ineasures of and , respectively. Observe that , and apply the theorem on exlerior angles of triangles to and to obtain and
Thus
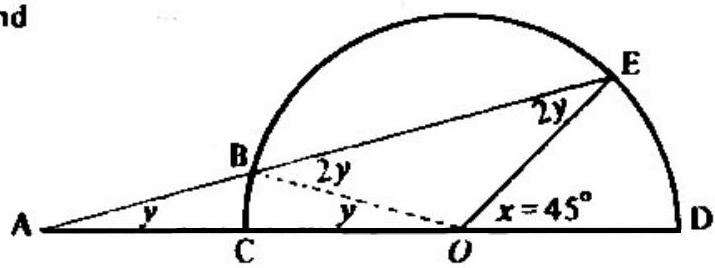
OR
Since the measure of an angle formed by two secants is half the difference of the intercepled arcs.