¶ 1980 AHSME Problem 22
Problem:
For each real number , let be the minimum of the numbers , , and . Then the maximum value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
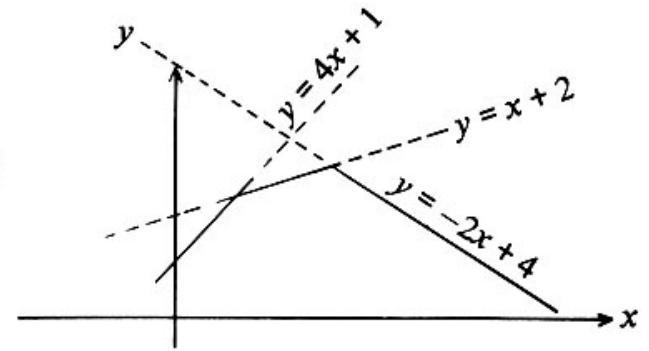
In the adjoining figure, the graphs of , and are drawn. The solid line represents the graph of the function . Its maximum occurs at the intersection of the lines and .
Thus and .