¶ 1981 AHSME Problem 18
Problem:
The number of real solutions to the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
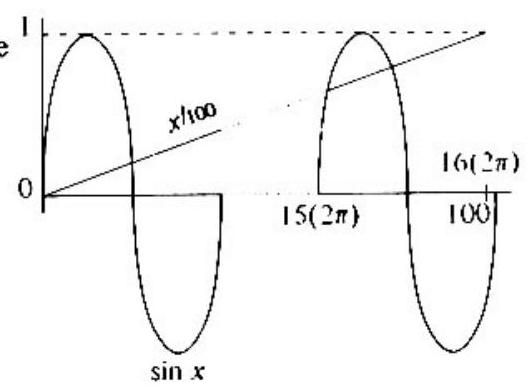
Since , the equation has an equal number of positive and negative solutions. Also is a solution. Furthermore, all positive solutions are less than or equal to , since .
Since , the graphs of and are as shown in the adjoining figure. Thus there is one solution to the given equation between 0 and and two solutions in each of the intervals from , to , .
The total number of solutions is, therefore,