Problem:
Let x,y and z be three positive real numbers whose sum is 1. If no one of these numbers is more than twice any other, then the minimum possible value of the product xyz is
Answer Choices:
A. 321
B. 361
C. 1254
D. 1271
E. none of these
Solution:
Let m=x0y0z0 be the minimum value. By symmetry, we may assume x0⩽ y0⩽z0. In fact z0=2x0, for if z0<2x0, then by decreasing x0 slightly, increasing z0 by the same amount, and keeping y0 fixed, we would get new values which still meet the constraints but which have a smaller product contradiction! To show this contradiction formally, let x1=x0−h and z1 =z0+h, where h>0 is so small that z1⩽2x1 also. Then x1,y0,z1 also meet all the original constraints, and
x1y0z1=(x0−h)y0(z0+h)=x0y0z0+y0[h(x0−z0)−h2]<x0y0z0
So z0=2x0,y0=1−x0−z0=1−3x0, and m=2x02(I−3x0). Also, x0⩽1−3x0⩽2x0, or equivalently, 51⩽x0⩽41. Thus m may be viewed as a value of the function f(x)=2x2(1−3x) on the domain D= {x∣∣∣∣∣51⩽x⩽41}. In fact, m is the smallest value of f on D, because minimizing f on D is just a restricted version of the original problem: for each x∈D, setting y=1−3x and z=2x gives x,y,z meeting the original constraints, and makes f(x)=xyz.
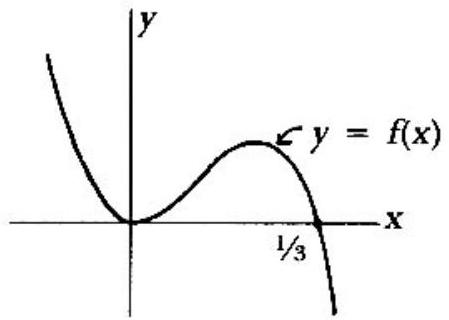
To minimize f on D, first sketch f for all real x. (See Figure.) Since f has a relative minimum at x=0(f(x) has the same sign as x2 for x<31), and cubics have at most one relative minimum, the minimum of f on D must be at one of the endpoints. In fact,
f(41)=321⩽f(51)=1254.
(If f had another relative minimum between its two zeros, say at point x=a, then the equation f(x)=f(a) would have at least 4 roots draw a sketch. But a cubic equation has at most three roots!)