¶ 1982 AHSME Problem 9
Problem:
A vertical line divides the triangle with vertices and in the -plane into two regions of equal area. The equation of the line is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
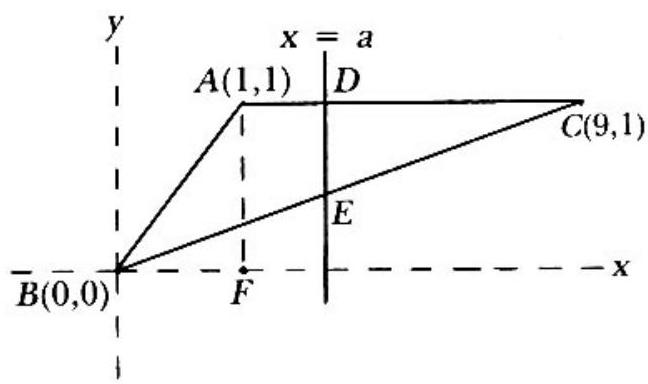
In the adjoining figure, is the given triangle and is the dividing line. Since Area , the two regions must each have area . Since the portion of to the left of the vertical line through vertex has area less than Area , the line is indeed right of as shown. Since the equation of the line is is (a, ).
Thus Area ,or . Then , and or . Since the line must intersect .