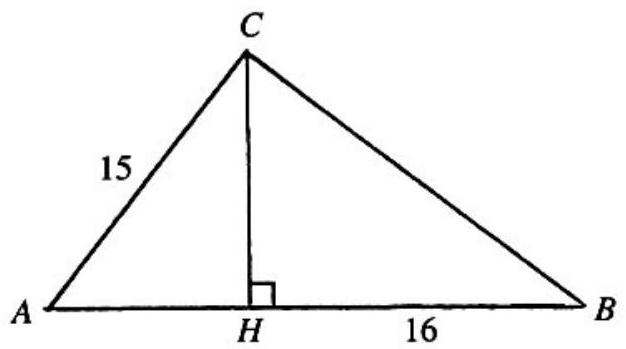
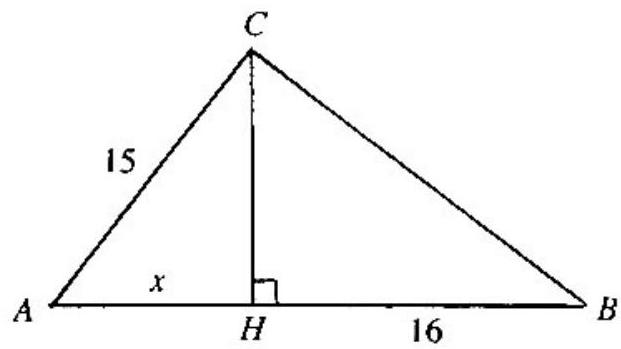
Problem:
A right triangle ABC with hypotenuse AB has side AC=15. Altitude CH divides AB into segments AH and HB, with HB=16. The area of △ABC is
Answer Choices:
A. 120
B. 144
C. 150
D. 216
E. 1445
Solution:
A leg of a right triangle is the geometric mean of the hypotenuse and the projection of the leg on the hypotenuse. Setting AH=x, it follows that
225=x(x+16),x2+16x−225=0,(x+25)(x−9)=0,x=9.
Thus AB=25,CH=152−92=12, and the area of △ABC is 21⋅25⋅12=150.