¶ 1985 AHSME Problem 13
Problem:
Pegs are put in a board unit apart both horizontally and vertically. A rubber band is stretched over pegs as shown in the figure, forming a quadrilateral. Its area in square units is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
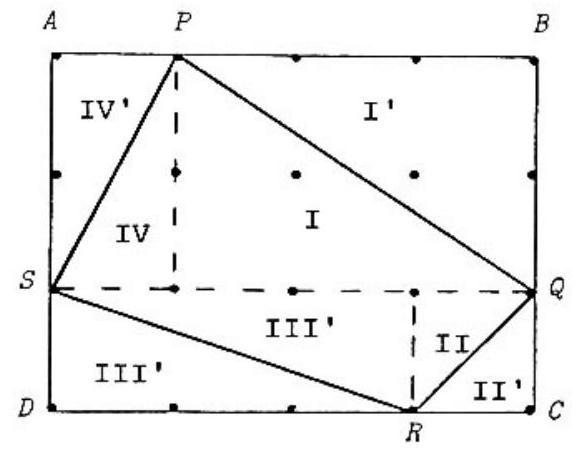
Method 1. Using the dotted horizontal and vertical lines shown as part of the figure, divide into right triangles, . Compute the area of each from the lengths of the legs and add.
Method 2. Surround PQRS by rectangle . Note that for each right triangle in Method , there is a second congruent triangle in . Thus
Method 3. Let be any polygon in the plane which has all its vertices at lattice points (points with both coordinates integers). can have any number of sides, and need not be convex, but different sides cannot cross each other. Then
where is the number of lattice points strictly inside and is the number on the boundary. Thus
This surprising formula is called Pick's Theorem.