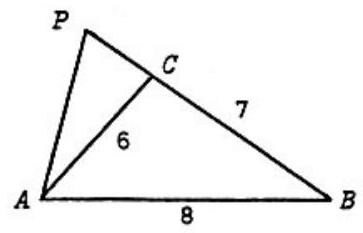
Problem:
In △ABC,AB=8,BC=7,CA=6 and side BC is extended, as shown in the figure, to a point P so that △PAB is similar to △PCA. The length of PC is
Answer Choices:
A. 7
B. 8
C. 9
D. 10
E. 11
Solution:
By the similarity of the two triangles, PBPA=PAPC=ABCA; hence PC+7PA=PAPC=86, yielding the two equations
6(PC+7)=8PA and 6PA=8PC
From these one obtains PC=9.