Problem:
Let c be a constant. The simultaneous equations
x−ycx+y=2=3
have a solution (x,y) inside Quadrant I if and only if
Answer Choices:
A. 0<c<3/2
B. c=−1
C. c>−1
D. c<3/2
E. −1<c<3/2
Solution:
Algebraic solution. Solving simultaneously, we obtain
x=c+15,y=c+13−2c
We wish to find all values of c for which x,y>0. First, x>0⇔c+1>0⇔c>−1. Next, given that c+1>0, then y>0⇔3−2c>0⇔3/2>c. Thus x,y>0⇔−1<c<3/2.
OR
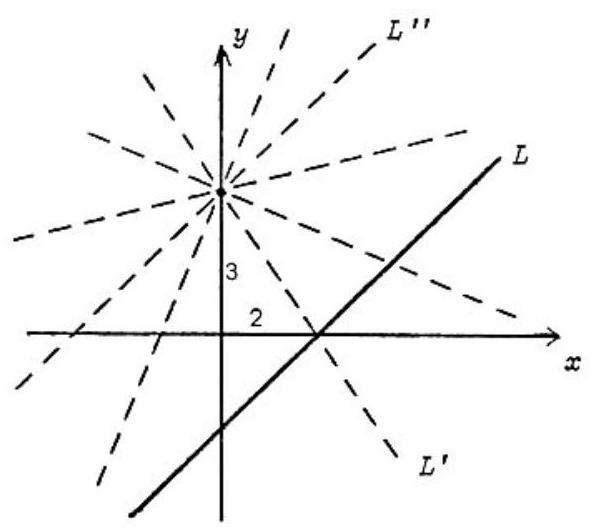
Geometric solution. We wish to find those values of c for which the lines x−y=2 and cx+y=3 intersect inside Quadrant I. The line x−y=2 has slope 1 and x-intercept 2, and is shown as L in the figure. The line cx+y=3 has y-intercept 3 and slope −c. Several possible choices for this line are shown dashed in the figure. For this line to intersect L in Quadrant I, it is necessary and sufficient to choose a slope between that of L′, which passes through (2,0), and that of L′′, which is parallel to L. Thus
−23<−c<1 or −1<c<23