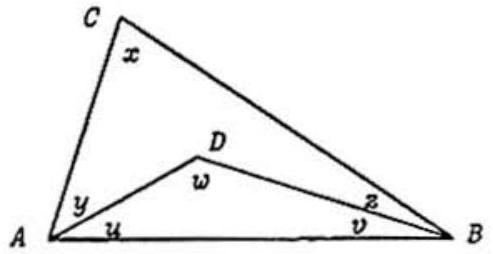
Problem:
In the △ABC shown, D is some interior point, and x,y,z,w are the measures of angles in degrees. Solve for x in terms of y,z and w.
Answer Choices:
A. w−y−z
B. w−2y−2z
C. 180−w−y−z
D. 2w−y−z
E. 180−w+y+z
Solution:
From the figure,
x=180−[(y+u)+(z+v)]=180−(y+z)−(u+v)=180−(y+z)−(180−w)=w−y−z
OR
Since ADBC is a quadrilateral, the sum of its interior angles is 360∘. (It does not matter that the interior angle at D is a reflex angle.) Thus
x+y+z+(360−w)=360x=w−y−z
.jpg)