Problem:
If sinx=3cosx then what is sinxcosx?
Answer Choices:
A. 61β
B. 51β
C. 92β
D. 41β
E. 103β
Solution:
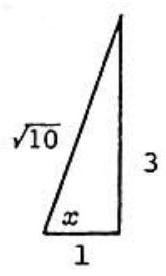
If sinx=3cosx then tanx=3. From the figure we conclude that
sinxcosx=10β3ββ
10β1β=103β
for any acute angle x. If xβ² is another angle with tanxβ²=3,xβ²βx is a multiple of Ο. Thus
sinxβ²=Β±10β3β,cosxβ²=Β±10β1β
So sinxβ²cosxβ² is still 3/10 (since sinxβ² and cosxβ² have the same sign ).
OR
Multiplying the given equation first by sinx and then by cosx yields
βsin2x=3sinxcosxcos2x=(1/3)sinxcosxβ
Adding gives
1=(10/3)sinxcosx
so sinxcosx=3/10.
