Problem:
In △ABC,AB=5,BC=7,AC=9 and D is on AC with BD=5. Find the ratio AD:DC.
Answer Choices:
A. 4:3
B. 7:5
C. 11:6
D. 13:5
E. 19:8
Solution:
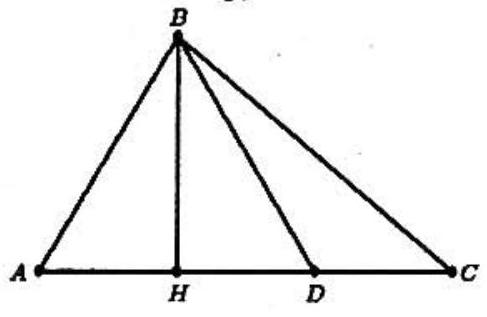
Apply the Law of Cosines to △BAC to find cosA=3019. Let H be the foot of the altitude from B. Then
AD=2⋅AH=2⋅ABcosA=319
Thus DC=38 and AD:DC=19:8.
OR
Let H be the foot of the altitude from B. Then, by the Pythagorean Theorem,
52−AH2=BH2=72−(9−AH)2
so AH=619,AD=2⋅AH=319. Thus AD:DC=AD:(9−AD)=19:8.