Problem:
An acute isosceles triangle, ABC, is inscribed in a circle. Through B and C, tangents to the circle are drawn, meeting at point D. If β ABC=β ACB=2β D and x is the radian measure of β A, then x=
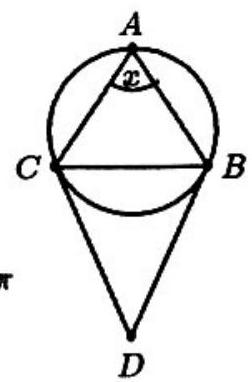
Answer Choices:
A. 73βΟ
B. 94βΟ
C. 115βΟ
D. 136βΟ
E. 157βΟ
Solution:
Angles BAC,BCD and CBD all intercept the same circular arc. Therefore β BCD=β CBD=x and β D=Οβ2x. The given condition now becomes 2Οβxβ=2(Οβ2x), which has the solution x=73βΟ.
OR
Let O be the center of the circle. Then β COB=2x and, from the sum of the angles of the quadrilateral COBD, we obtain 2x+β D=Ο. The conditions of the problem yield x+4β D=Ο to be the sum of the angles of β³ABC. Solve these two equations in x and β D simultaneously to find x=3Ο/7.
Query. What is x if β³ABC is an obtuse isosceles triangle?
