Problem:
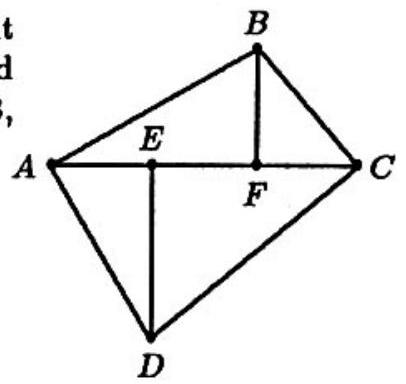
In the figure, ABCD is a quadrilateral with right angles at A and C. Points E and F are on AC, and DE and BF are perpendicular to AC. If AE=3, DE=5 and CE=7, then BF=
Answer Choices:
A. 3.6
B. 4
C. 4.2
D. 4.5
E. 5
Solution:
Since ∠BAF and ∠ADE are both complementary to ∠CAD they must be equal. Thus, △BAF∼△ADE so AFBF=DEAE, or 3+EFBF=53. By an analogous argument, △BCF∼△CDE,CFBF=DECE, and 7−EFBF=57. Solve these two equations simultaneously to obtain BF=4.2.
OR
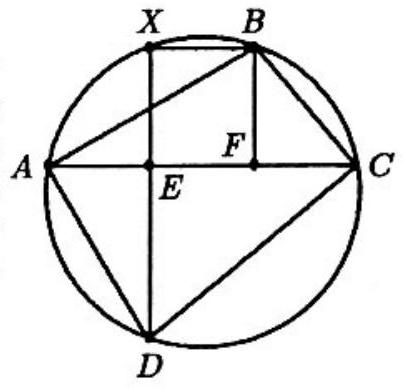
Note that ABCD is a cyclic quadrilateral since opposite angles are supplementary. Extend DE to X on the circumcircle. Since ∠DAB subtends the same arc as ∠DXB,BFEX is a rectangle and BF=EX. We can consider AC and DX as intersecting chords in a circle and use DE⋅EX= AE⋅EC to find BF=EX=DEAE⋅EC=521.