Problem:
The graph, G, of y=log10x is rotated 90∘ counter-clockwise about the origin to obtain a new graph G′. Which of the following is an equation for G′?
Answer Choices:
A. y=log10(9x+90)
B. y=logz10
C. y=x+11
D. y=10−x
E. y=10x
Solution:
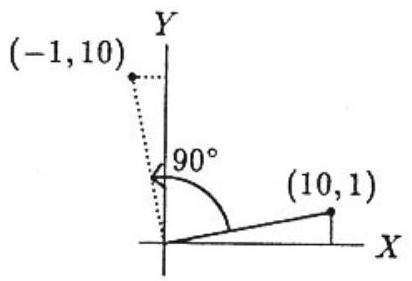
The point (x,y) is on the graph of G′ if and only if the point (y,−x) is on the graph of G, so −x=log10y. This last equation is equivalent to y=10−x, which is an equation for G′. Since (x,y)=(10,1) is on G, it follows that (x,y)=(−1,10) must be on G′, which shows that no other choice is correct.
Note. The 90∘ rotation relates each (x,y) on G′ to the point (xcos90∘+ysin90∘,−xsin90∘+ycos90∘) on G.