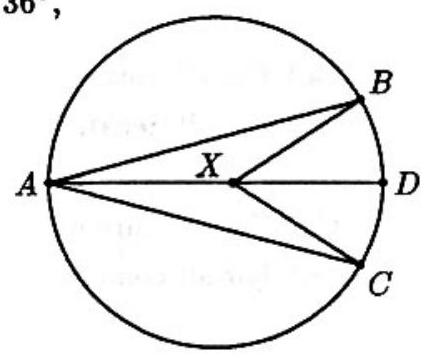
Problem:
Points A,B,C and D are on a circle of diameter 1, and X is on diameter AD. If BX=CX and 3β BAC=β BXC=36β, then AX=
Answer Choices:
A. cos6βcos12βsec18β
B. cos6βsin12βcsc18β
C. cos6βsin12βsec18β
D. sin6βsin12βcsc18β
E. sin6βsin12βsec18β
Solution:
The center of the circle is not X since 2β BACξ =β BXC. Thus AD bisects β BXC and β BAC. (Why?) Since β ABD=90β and AD=1, it follows that AB=ADcosβ BAD=cos21ββ BAC=cos6β. Note that β AXB=162β and β ABX=12β. By the Law of Sines,
sinβ AXBABβ=sinβ ABXAXβ so sin162βcos6ββ=sin12βAXβ.
Since sin162β=sin18β, we have
AX=sin18βcos6βsin12ββ=cos6βsin12βcsc18β.
