Problem:
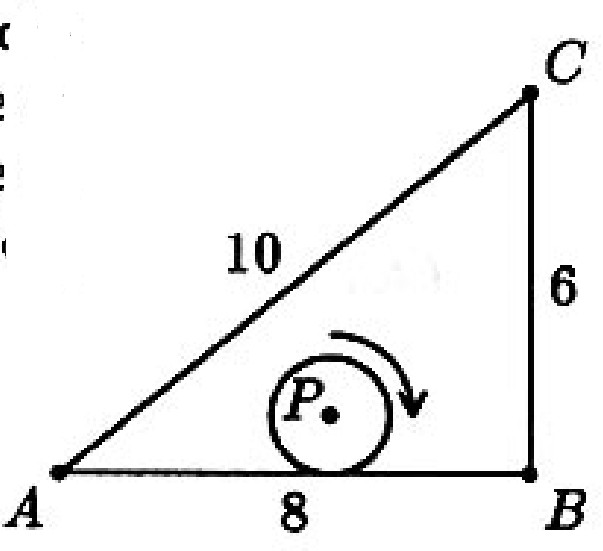
The sides of β³ABC have lengths 6,8 and 10. A circle with center P and radius 1 rolls around the inside of β³ABC, always remaining tangent to at least one side of the triangle. When P first returns to its original position, through what distance has P traveled?
Answer Choices:
A. 10
B. 12
C. 14
D. 15
E. 17
Solution:
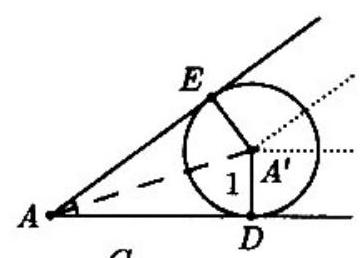
When the circle is closest to A with its center P at Aβ², let its points of tangency to AB and AΛCΛ be D and E, respectively. The path parallel to AB is shorter than AB by AD plus the length of a similar segment at the other end. Now AD=AE=cot2Aβ. Similar reasoning at the other vertices shows that the length of the path of P is
AB+BC+CAβ2cot2Aββ2cot2Bββ2cot2Cβ.
Since cot2Aβ=sinA1+cosAβ=53β1+54ββ=3, and similarly cot2Bβ=1 and cot2Cβ=2, the length of the path is 8+6+10β6β2β4=12.
OR
The locus of P is a triangle Aβ²Bβ²Cβ² similar to triangle ABC. Calculating as above, we have Aβ²Bβ²=ABβcot2Aββcot2Bβ=8β3β1=4=21βAB, so the linear dimensions of β³Aβ²Bβ²Cβ² are half those of β³ABC, and its perimeter is 28+6+10β=12.
OR
The locus, β³DEF, of the center of the rolling circle is similar to β³ABC, so we label its sides 3x,4x and 5x, for some x>0. The area of β³ABC is (AB)(BC)/2=24. Partition β³ABC into three trapezoids of altitude 1 and β³DEF, and compute the area of β³ABC in terms of x:
[ABC]β=[DABE]+[EBCF]+[FCAD]+[DEF]β=21β(1)(4x+8)+21β(1)(3x+6)+21β(1)(5x+10)+6x2β=6x2+6x+12.β
Solve 6x2+6x+12=24 for the positive root, x=1, to find that the perimeter of β³DEF is 3x+4x+5x=12x=12.
Challenge. Prove that for any triangle and for any circle that rolls around inside the triangle, the perimeter of the triangle, which is the locus of the center of the circle, is the perimeter of the original triangle diminished by the perimeter of the similar triangle, which circumscribes the circle.
.jpg)