Problem:
In triangle ABC,AB=AC. If there is a point P strictly between A and B such that AP=PC=CB, then ∠A=
Answer Choices:
A. 30∘
B. 36∘
C. 48∘
D. 60∘
E. 72∘
Solution:
Let ∠A=x∘. Then ∠PCA=x∘ since AP=PC. By the exterior angle theorem, ∠BPC=∠A+∠PCA=2x∘. Since PC=CB, it follows that ∠B=2x∘. Thus ∠ACB=2x∘ since AB=AC. Therefore, x+2x+2x=180, or ∠A=x∘=36∘.
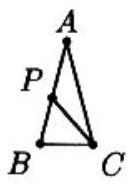
.jpg)