Problem:
Points A,B and C on a circle of radius r are situated so that AB=AC,AB>r, and the length of minor arc BC is r. If angles are measured in radians, then AB/BC=
Answer Choices:
A. 21βcsc41β
B. 2cos21β
C. 4sin21β
D. csc21β
E. 2sec21β
Solution:
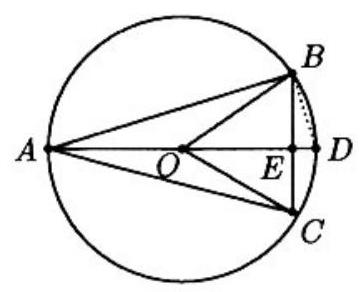
Draw and label the figure as shown, where O is the center of the circle. In radians, β BOC= r/r=1, so β BAC=1/2 and β BAE=1/4. Since BEβ₯EA, it follows that
BCABβ=21βBEABβ=21βcscβ BAE=21βcsc41β.
OR
Since β BAC=21β, it follows that β ACB=21β(Οβ21β)=2Οββ41β. The length of a chord subtended by the inscribed angle Ξ² in a circle of radius r is 2rsinΞ², so
βAB=2rsinβ ACB=2rsin(2Οββ41β)=2rcos41ββBC=2rsinβ BAC=2rsin21β=4rsin41βcos41ββ
Therefore, BCABβ=4rsin41βcos41β2rcos41ββ=2sin41β1β=21βcsc41β.
OR
By the Law of Sines, BCABβ=sinAsinCβ. But 2β C+β A=Ο, so β C=2Οββ2β Aβ and sinC=cos2Aβ. Since β A=21β,
BCABβ=sinAsinCβ=2sin2Aβcos2Aβcos2Aββ=2sin2Aβ1β=21βcsc2Aβ=21βcsc41β.
.jpg)