¶ 1995 AHSME Problem 28
Problem:
Two parallel chords in a circle have lengths and , and the distance between them is . The chord parallel to these chords and midway between them is of length where is
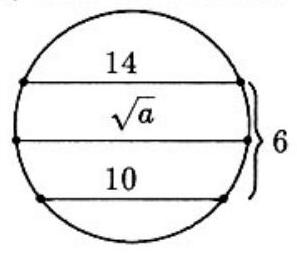
Answer Choices:
A.
B.
C.
D.
E.
Solution:
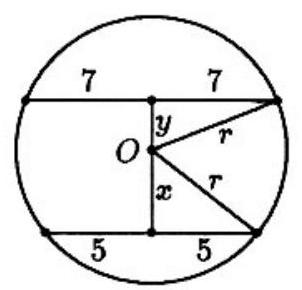
Let be the distance from the center of the circle to the chord of length , and let be the distance from to the chord of length . Let be the radius. Then,
Therefore, .
If the chords are on the same side of the center of the circle, . If they are on opposite sides, . But implies that , which is impossible. Hence and . Solve these equations simultaneously to get and . Thus, , and the chord parallel to the given chords and midway between them is units from the center. If the chord is of length , then , and .
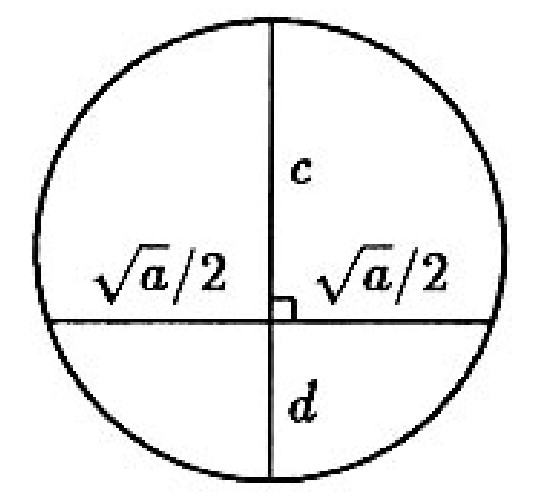
The diameter perpendicular to the chords is divided by the chord of length into segments with lengths and as shown.
Then
Treat the chords units above and units below similarly:
Adding the last two equations, we get . Thus, so .