Problem:
Given that x2+y2=14x+6y+6, what is the largest possible value that 3x+4y can have?
Answer Choices:
A. 72
B. 73
C. 74
D. 75
E. 76
Solution:
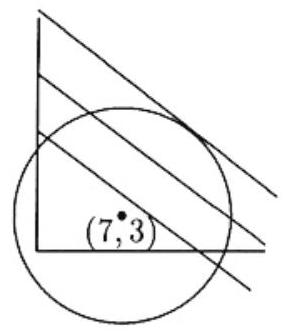
The equation x2+y2=14x+6y+6 can be written
(x−7)2+(y−3)2=82,
which defines a circle of radius 8 centered at (7,3). If k is a possible value of 3x+4y for (x,y) on the circle, then the line 3x+4y=k must intersect the circle in at least one point. The largest value of k occurs when the line is tangent to the circle, and is therefore perpendicular to the radius at the point of tangency. Because the slope of the tangent line is −3/4, the slope of the radius is 4/3. It follows that the point on the circle that yields the maximum value of 3x+4y is one of the two points of tangency,
x=7+53⋅8=559,y=3+54⋅8=547,
or
x=7−53⋅8=511,y=3−54⋅8=−517.
The first point of tangency gives
3x+4y=3⋅559+4⋅547=5177+5188=73,
and the second one gives 3x+4y=533−568=−7. Thus 73 is the desired maximum, while −7 is the minimum.
OR
Suppose that k=3x+4y is a possible value. Substituting y=(k−3x)/4 into x2+y2=14x+6y+6, we get 16x2+(k−3x)2=224x+24(k−3x)+96, which simplifies to
25x2−2(3k+76)x+(k2−24k−96)=0. (1)
If the line 3x+4y=k intersects the given circle, the discriminant of (1) must be nonnegative. Thus we get (3k+76)2−25(k2−24k−96)≥0, which simplifies to
(k−73)(k+7)≤0.
Hence −7≤k≤73.