¶ 1996 AHSME Problem 28
Problem:
On a rectangular parallelepiped, vertices , and are adjacent to vertex . The perpendicular distance from to the plane containing , and is closest to
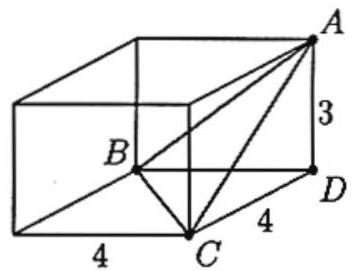
Answer Choices:
A.
B.
C.
D.
E.
Solution:
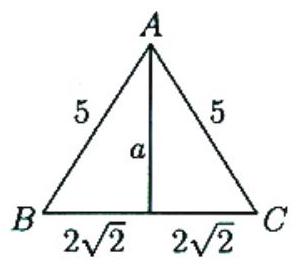
Let be the required distance. Find the volume of pyramid as a third of the area of a triangular base times the altitude to that base in two different ways, and equate these volumes. Use the altitude to to find that the volume is 8 . Next, note that is the length of the altitude of the pyramid from to . Since the sides of are 5,5 , and , by the Pythagorean Theorem the altitude to the side of length is . Thus, the area of is , and the volume of the pyramid is . Equating the volumes yields
Imagine the parallelepiped embedded in a coordinate system as shown in the diagram. The equation for the plane (in intercept form) is . Thus, it can be expressed as . The formula for the distance from a point to the plane is given by
which in this case is
.jpg)