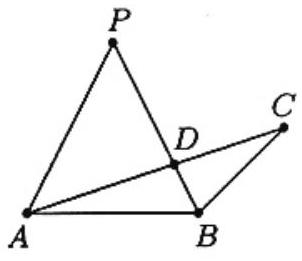
Problem:
Triangle ABC and point P in the same plane are given. Point P is equidistant from A and B, angle APB is twice angle ACB, and AC intersects BP at point D. If PB=3 and PD=2, then AD⋅CD=
Answer Choices:
A. 5
B. 6
C. 7
D. 8
E. 9
Solution:
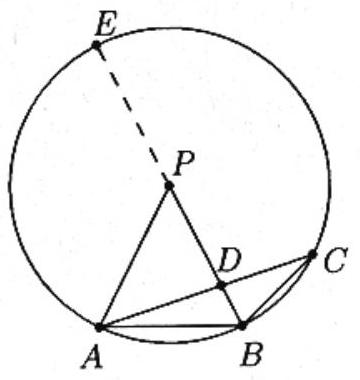
Construct a circle with center P and radius PA. Then C lies on the circle, since the angle ACB is half angle APB. Extend BP through P to get a diameter BE. Since A,B,C, and E are concyclic,
AD⋅CD=ED⋅BD=(PE+PD)(PB−PD)=(3+2)(3−2)=5.
OR
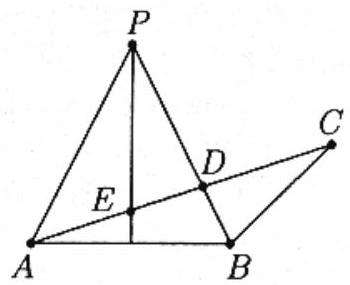
Let E denote the point where AC intersects the angle bisector of angle APB. Note that △PED∼ △CBD. Hence DE/2=1/DC so DE⋅DC=2. Apply the Angle Bisector Theorem to △APD to obtain
DEEA=PDPA=23.
Thus DA⋅DC=(DE+EA)⋅DC=(DE+1.5DE)⋅DC=2.5DE⋅DC=5.