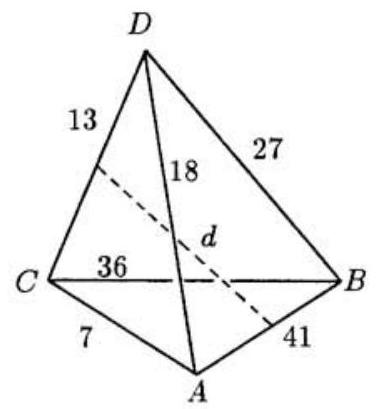
Problem:
Let ABCD be a tetrahedron with AB=41, AC=7,AD=18,BC=36,BD=27, and CD=13, as shown in the figure. Let d be the distance between the midpoints of edges AB and CD. Find d2.
Solution:
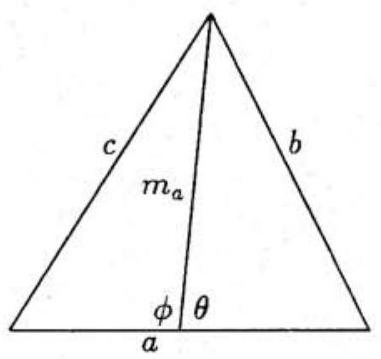
We first show that if a,b and c are the three sides of a triangle and maβ is the median to side a, then
ma2β=41β(2b2+2c2βa2)(1)
We then apply (1) three times in order to find the desired d2.
To prove (1), consider the figure shown below. Apply the Law of Cosines to each of the two smaller triangles to get
ma2ββ=21β(ma2β+ma2β)=21β[(c2β41βa2+amaβcosΟ)+(b2β41βa2+amaβcosΞΈ)]=41β(2b2+2c2βa2)+21βamaβ(cosΟ+cos(ΟβΟ))=41β(2b2+2c2βa2)β
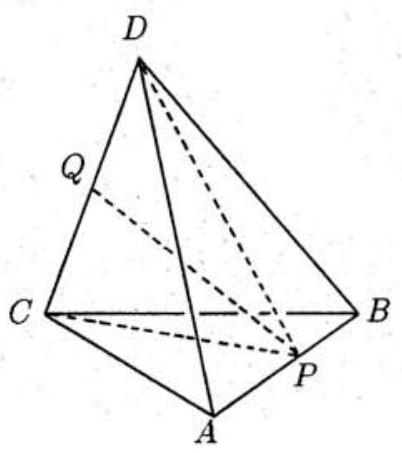
Next, in the tetrahedron shown below, let P be the midpoint of AB and Q be the midpoint of CD. We apply (1) to find (PC)2 (since PC is a median of β³ABC) and (PD)2 (since PD is a median of β³ABD). We find
(PC)2=41β[2(AC)2+2(BC)2β(AB)2]=41009β
and
(PD)2=41β[2(AD)2+2(BD)2β(AB)2]=4425β
Finally, we again use (1) to find d2=(PQ)2 from β³CDP:
(PQ)2=41β[2(PC)2+2(PD)2β(CD)2]=137β
OR
Introduce the vectors u,v and w to denote the directed edges from A. (See the accompanying figure.) The other three edges, with orientations as indicated, are given by uβv, uβw and vβw. Moreover, the vector from A to the midpoint of AB is 21βu and the vector from A to the midpoint of CD is 21β(v+w). Consequently, the vector from the midpoint of CD to the midpoint of AB is 21βuβ21β(v+w). We seek the square of the length of this last vector.
Recalling that for a vector x,β£xβ£2=xβ
x, we have
d2=41β(uβvβw)β
(uβvβw)=41β(β£uβ£2+β£vβ£2+β£wβ£2β2uβ
vβ2uβ
w+2vβ
w)(1)
To find uβ
v,uβ
w and vβ
w, note that β£xβyβ£2=β£xβ£2+β£yβ£2β2xβ
y, which implies
2xβ
y=β£xβ£2+β£yβ£2ββ£xβyβ£2(2)
Applying (2) to (1) yields the general formula
d2=41β(β£vβ£2+β£wβ£2+β£uβvβ£2+β£uβwβ£2ββ£uβ£2ββ£vβwβ£2)(3)
The given measurements yield d2=137β.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)