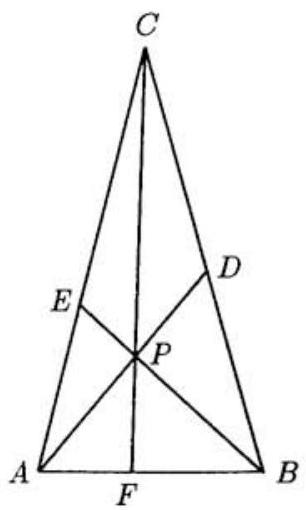
Problem:
Point P is inside △ABC. Line segments APD,BPE and CPF are drawn with D on BC,E on CA, and F on AB (see the figure at the right). Given that AP=6,BP=9,PD=6,PE=3 and CF=20, find the area of △ABC.
Solution:
We are given length information about the three segments through P. Our strategy is to translate one of these segments to form a new triangle (inside of △ABC ) for which we know all three sides, and hence the area. We then multiply this area by an appropriate ratio to obtain the area of △ABC.
We first find the lengths of CP and PF. To this end, observe that
Area(△BAC)Area(△BPC)=ADPD=6+66=21(1)
and
Area(△ABC)Area(△APC)=BEPE=3+93=41(2)
Thus
CFPF=Area(△ACB)Area(△APB)=Area(△ACB)Area(△ACB)−Area(△APC)−Area(△BPC)=1−41−21=41(3)
Since CF=20, it follows that PF=5 and CP=15. Furthermore,
CDBD=Area(△ACD)Area(△ADB)=Area(△PDC)Area(△PDB)=Area(△ACD)−Area(△PDC)Area(△ADB)−Area(△PDB)=Area(△ACP)Area(△APB)=1,
where the last equality results from dividing equation (3) by equation (2).
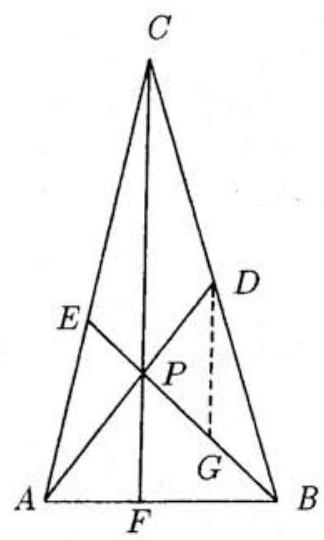
Next construct DG parallel to CF, with G on PB as shown. We show that △GDP is a right triangle with sides of 29,6 and 215 and then show that the area of △GDP is 81 of the area of △ABC. It will then follow that the desired answer is 8⋅227=108.
To establish the above claims, first note that △BDG∼△BCP. Since BD=21BC, the sides of these two triangles are in a ratio of 1:2. It follows that DG=21PC=215 and PG=GB=21PB=29. Since PD=6 was given, we see that △GDP is a right triangle as claimed. Next note that
Area(△GBD)Area(△PBC)=(12)2=4 and Area(△GPD)Area(△GBD)=PGBG=1
Using these ratios with (1) gives
Area(△ABC)=Area(△PBC)Area(△ABC)⋅Area(△GBD)Area(△PBC)⋅Area(△GPD)Area(△GBD)⋅Area(△GPD)=2⋅4⋅1⋅227=108
Note. Implicit in this solution is a method for constructing △ABC with straightedge and compass from the given data. The reader is invited to explore the conditions such data must satisfy in order to ensure that △ABC exists (and is unique).
OR
Let P=(0,0),D=(6,0),A=(−6,0),E=(h,k) and B=(−3h,−3k). Solving the equations for AE and BD simultaneously, we find C=(3h+12,3k). Next, the coordinates of F can be found by solving the equations of CP and AB simultaneously; the result is F=(−4−h,−k). Finally, solving the equations h2+k2=9 and (4+h)2+k2=25 (arising from PE=3 and CF=20, respectively) one finds that h=0 and k=3. Once we have the coordinates of A,B and C, we can find that the area of △ABC is 108.
The problems on this page are the property of the MAA's American Mathematics Competitions