Problem:
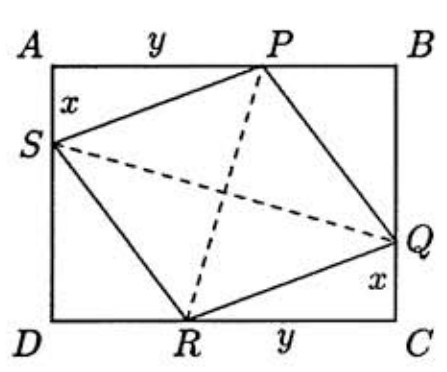
Rhombus PQRS is inscribed in rectangle ABCD so that vertices P,Q,R, and S are interior points on sides AB,BC,CD, and DA, respectively. It is given that PB=15,BQ=20,PR=30, and QS=40. Let nmβ, in lowest terms, denote the perimeter of ABCD. Find m+n.
Solution:
Let x and y stand for QC and RC respectively, and note that these are also the lengths of SA and PA as well. The diagonals of a rhombus bisect each other at right angles, hence PQRS and its diagonals divide the rectangle into eight right triangles. Six of these triangles have side lengths of 15,20, and 25, while the other two have sides of length x,y, and 25. Summing the areas of these eight pieces, we find that
6(150)+2(21βxy)β=Area(ABCD)=(20+x)(15+y)β
which leads to 3x+4y=120. Combining this with x2+y2=625 leads to the quadratic equation
5x2β144x+880=0
Factoring gives (5xβ44)(xβ20)=0. Note that x cannot be 20 since this would imply BC=40, which is inconsistent with PR=30. Hence x=44/5,y=117/5, and the perimeter of rectangle ABCD is 2(15+20+x+y)=5672β.
Thus, m+n=677β.
OR
Let x and y stand for AS and AP respectively, and let O denote the intersection of PR and QSβ. Let F and G, respectively, be the feet of the perpendiculars from O to AB and AD. Then β FOP=β GOS. Let ΞΈ be the measure of each of these angles. We then have
cosΞΈ=20(y+15)/2β=15(x+20)/2β(*)
from which we obtain 3yβ4x=35. The equation 3x+4y=120 can be obtained as in the previous solution. Solving the linear equations
3x+4yβ4x+3yβ=120=35β
simultaneously gives x=44/5 and y=117/5. The perimeter of ABCD is thus 2(15+20+x+y)=5672β.
Note. From equation (β) it follows that all rectangles that circumscribe a given rhombus have the same shape.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)