¶ 1991 AIME Problem 15
Problem:
For positive integer , define to be the minimum value of the sum
where are positive real numbers whose sum is . There is a unique positive integer for which is also an integer. Find this .
Solution:
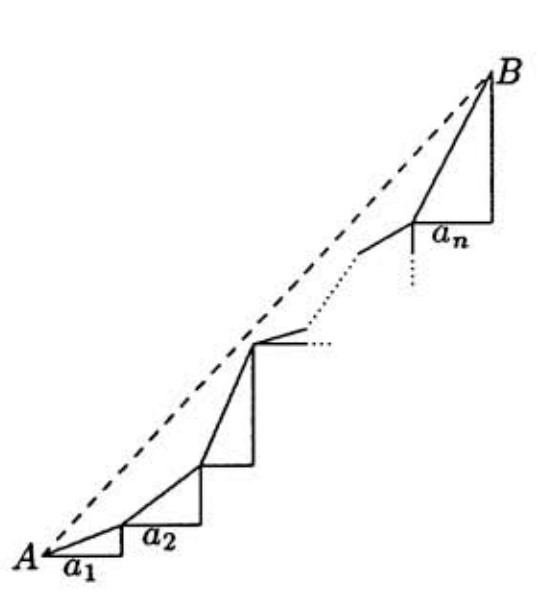
We interpret each term
as the length of the hypotenuse of a right triangle with legs of length and . Put the triangles together in a "staircase" arrangement as shown in the diagram, and let and be the initial and terminal points of the broken path formed by the hypotenuses. The distance from to is
while the sum is the length of the path from to formed by the hypotenuses of the triangles. It follows immediately that , and that equality is obtained by choosing the so that the broken path is actually a straight line. Thus is the minimum possible value of the given sum. When is an integer, the equation implies that
and
Solving this system yields and .
The problems on this page are the property of the MAA's American Mathematics Competitions