Problem:
Rectangle ABCD has sides AB of length 4 and CB of length 3. Divide AB into 168 congruent segments with points A=P0,P1,…,P168=B, and divide CB into 168 congruent segments with points C=Q0,Q1,…,Q168=B. For 1≤k≤167, draw the segments PkQk. Repeat this construction on the sides AD and CD, and then draw the diagonal AC. Find the sum of the lengths of the 335 parallel segments drawn.
Solution:
By symmetry, the sum of the lengths of the 335 segments is equal to
AC+2k=1∑167PkQk.
For 1≤k≤167 we have PkB=AB(1−168k) and BQk=BC(1−168k). It follows that △PkBQk∼△ABC, so PkQk=AC(1−168k). Thus the sum of the 335 segments is
AC(1+2k=1∑167(1−168k))=5(1+1682j=1∑167j)=5(1+16822167⋅168)=840.
OR
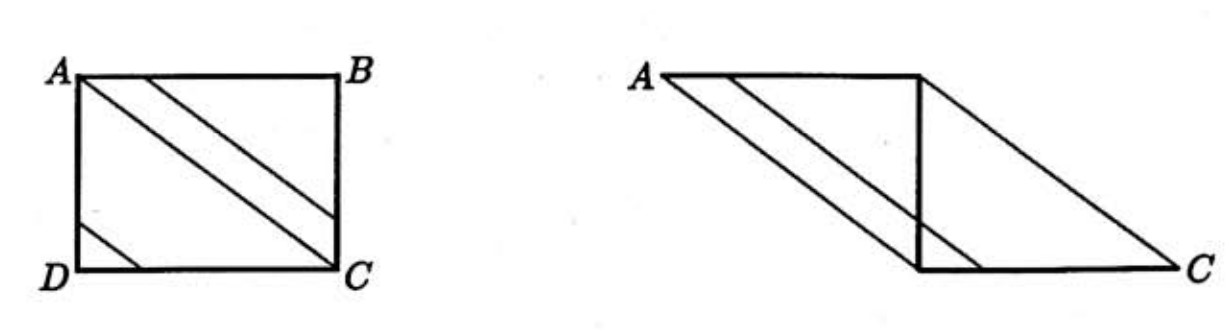
Cut the rectangle along diagonal AC, then reposition △ABC so vertices B and C of △ABC are coincident with vertices A and D, respectively, of △ADC. The resulting figure is a parallelogram. In doing this cutting and repositioning we see that, except for diagonal AC which has length 5, all of the other 334 segments can be grouped into pairs whose lengths sum to 5. (See figure.) Hence the desired sum is 5+167⋅5=840.
The problems on this page are the property of the MAA's American Mathematics Competitions