Problem:
How many real numbers x satisfy the equation 51βlog2βx=sin(5Οx)?
Solution:
Since β£sinΞΈβ£β€1 for all real ΞΈ, we need only consider those values of x for which
β£β£β£β£β£β51βlog2βxβ£β£β£β£β£ββ€1
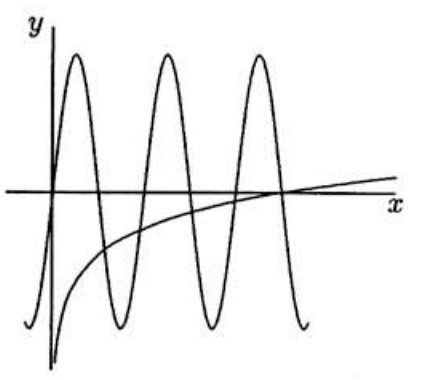
This inequality is satisfied by all values of x between 321β and 32, inclusive. We first consider 321ββ€x<1. For such x we have β1β€51βlog2βx<0, while sin5Οxβ€0 only for 51ββ€xβ€52β and 53ββ€xβ€54β. It follows that the graphs of y=51βlog2βx and y=sin5Οx meet at 4 points for 321ββ€x<1. (See accompanying figure.) When 1<xβ€32, we have 0<51βlog2βxβ€1 while sin5Οxβ₯0 only for 52kββ€xβ€52k+1β(k=3,4,β¦,79). The graphs of the two functions intersect at 2 points on each of these 77 intervals, giving 154 points of intersection for 1<xβ€32. Since both functions take on the value 0 when x=1, we have a total of 4+154+1=159β solutions to the equation.
The problems on this page are the property of the MAA's American Mathematics Competitions